Topologie Federmann
Úvod
Krok za krokem se věnujeme topologii, která je v mnohém podobna a přitom tak odlišná od ostatních Topologii. Doposud vše bylo zaměřeno na náhradní schéma tranzistoru, chování vstupní diferenciální dvojice a Udif, které je odvozeno od rozdílu vstupního a výstupního napětí.
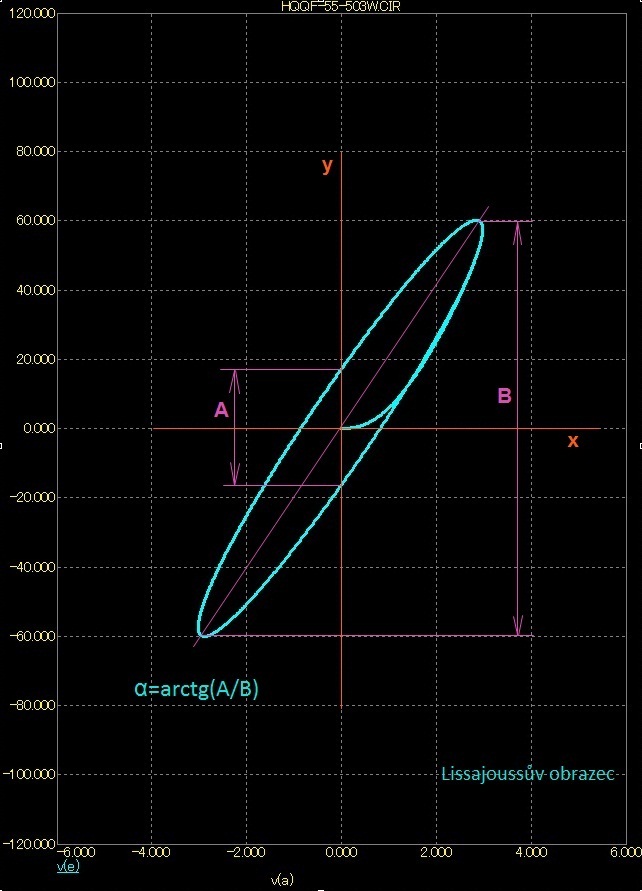
Udif a jeho odvození
Několik výpočtů:
- Udif=Ua-Ub
- Au=Uc/Ua
- Au*=Uc/Udif
- α=arctg(A/B)
Vysvětlení pojmů:
- • Au=napěťové zesílení zesilovače
- • Au*=napěťové zesílení zesilovače bez zpětné vazby
- • Ua= vstupní napětí
- • Ub=Uc *β
- • Uc=výstupní napětí
- • β=přenos zpětnovazebního děliče• α=zpoždění zesilovače
Výpočty:
Pro stejnosměrný signál vyjde konkrétní hodnota napětí Udif
- Au*=Uc/Udif
- Udif=Ua-Ub
- Udif=Ua- Uc *β
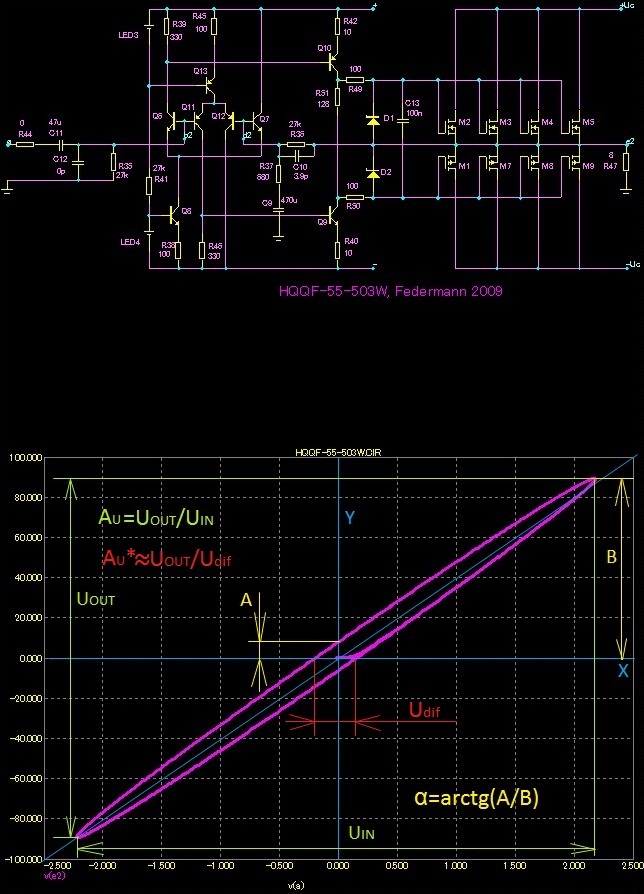
Pro střídavý signál vyjde obdobná hodnota napětí Udif
Vysvětlení pojmů:
- • Ua= U1*sinus (ωt+0)
- • Uc=U2*sinus (ωt+ α)
Výpočty:
- Udif= U1*sinus (ωt+0) - U2*sinus (ωt+ α)*β
- Udif = U2*sinus (ωt+ α)/Au*
- U2*sinus (ωt+ α)/Au*= U1*sinus (ωt+0)- U2*sinus (ωt+ α)*β
Odtud vidíme, že Udif je funkcí:
- 1. Vstupního napětí
- 2. Fázového posuvu α
- 3. Výstupního napětí U2
- 4. Přenosem zpětné vazby β
Při jistém zjednodušení můžeme napsat:
- • Au=U2/U1
- • β≈U1/U2
- • U2*β≈U1
Dále můžeme pokračovat a napsat
Udif≈U1*sin α
Odtud je patrné že:
- 1. Pokud zesílení otevřené smyčky s frekvencí neklesá, bude fázový posun α konstantní a blízký 0°.
- 2. V okamžiku, kdy začne zesílení otevřené smyčky s frekvencí klesat, začne úhel α narůstat.
- 3. Sinus úhlu α je funkci převrácené hodnoty rezervy zisku Au*-Au.
Udif bez signálu
Velmi důležitou hodnotou je velikost Udif bez vybuzení, bez signálu. Jde o klidový pracovní bod, proto dnes ještě chvíli u Udif zůstaneme.
Udif je nepřímo závislé na velikosti celkové zpětné vazby, ale také na zanesených napěťových chybách. Napěťové chyby nám zanese nestejná charakteristika vstupních tranzistorů, jejich rozdílný zesilovací činitel a také velikost vstupního proudu.
Největší chybu nám zanese ´úbytek napětí na odporech připojených do bází vstupních tranzistorů. Aby byla chyba, co nejmenší měly by být odpory stejné, pak se nám projeví jen rozdílný zesilovací činitel a teplotní závislosti.
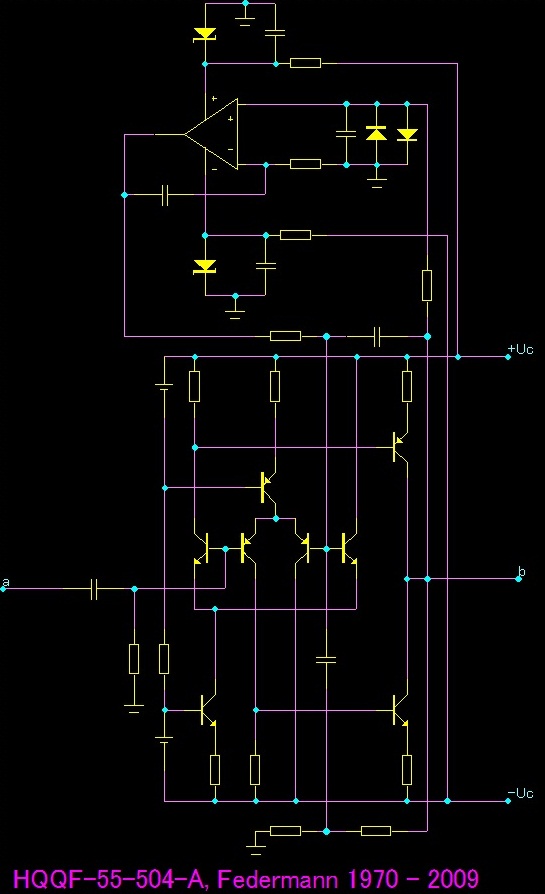
P-I regulátor
Velmi elegantním a jednoduchým zapojením, které nám hlídá polohu pracovního bodu je P-I (proporcionálně – integrační) regulátor, který snímá napětí na výstupu zesilovače. Vstupní část regulátoru tvoří integrační článek, který je dále připojen na vstup integrátoru. Časové konstanty jsou voleny řádově jednotky sekund. Výstup integrátoru je připojen přes patřičný odpor na invertující vstup zesilovače a řídí polohu pracovního bodu.
Vhodnou volbou OZ můžeme dosáhnout bez dalších nastavovacích prvků, chybové výstupní napětí zesilovače daleko pod 1mV, stejně tak velikost Vdif.
Hlavní důvod použití P-I regulátoru
P-I regulátor mnozí používají k dosažení minimálního ss napětí na reproduktoru. Jak je vidět z vlastností Udif, je v Topologii Federmann hlavním důvodem použití P-I regulátoru dosažení minimálního klidového napětí Udif.
Dosažením minimálního klidového Udif dosáhneme maximální hodnoty zisku vstupní diferenciální dvojice, ale také zajistíme jeho maximální symetrii a linearitu. Jak je vidět, přesné nastavení minimálního Udif á vliv na linearitu celého zesilovače, jeho šumové vlastnosti, ale také frekvenční rozsah.
P-I regulátor zajistí dlouhodobou i tepelnou stabilitu pracovního budu a nemusí jít pouze o koncový stupeň, neboť zde napsané platí zcela obecně pro každé zapojení, které má na vstupu diferenciální dvojici.

Podívejte se na články se stejnou tématikou.
Úvod
Před nedávnem jsem slíbil konstrukci Jednodeskového Nf zesilovače. Čekal jsem projevení jistého zájmu, ale zdaleka nebyl takový, jak by se dalo u této konstrukce čekat. Je mnoho konstrukcí, ať již s integrovanými obvody či sestavené s klasických součástek. Ve většině případů jde o naprosto oddělené části, jako koncový stupeň, korekční zesilovač, předzesilovač a zdroj.
Návrh a cíle
Návrh jednodeskového zesilovače by měl některé části sloučit a konstrukci tak výrazně zjednodušit. Konstrukce by měla být jednoduchá, dostatečně kvalitní při zachování příznivé ceny, čímž by si měla získat značnou řadu příznivců. Zesilovač by měl sloužit jako samostatný, ale zároveň by měl umožňovat implementovat do reproduktorové skříně, čímž vznikne řada dalších možností.
Zapojení
Korekce
Zapojení vychází z již osvědčené konstrukce HQQF-55-502. Koncový stupeň je zapojen jako zpětnovazební Baxandallův korektor. Jak již bylo avizováno, jde o pokračování Korekčního zesilovače „zapojení Federmann“, který si pro své vynikající vlastnosti získal řadu příznivců.
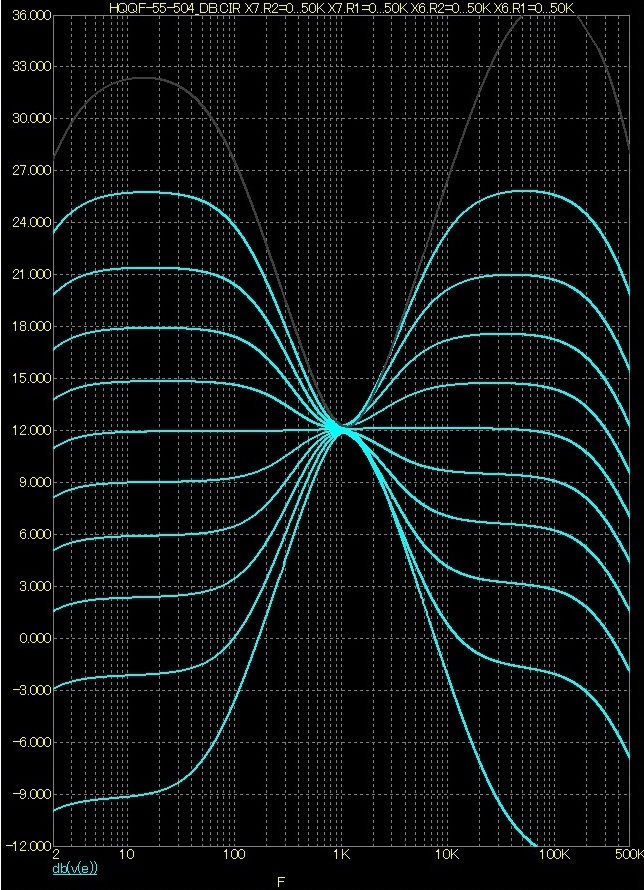
Korekční zesilovač „zapojení Federmann“ ve své původní podobě disponoval rozsahem regulace zisku na krajích akustického pásma přes 20dB. Nyní jsem rozsah regulace zisku upravil na dvě hodnoty. Zákazník si může vybrat, zda požaduje rozsah regulace zisku 20dB či referuje rozsah regulace jen 15dB.
Výkon
Stejně jak lze vybrat rozsah regulace zisku je možno vybírat mezi verzí na napájecí napětí 25 až 50V, případně i více. Výstupní výkon 50 až 250W na kanál. Obdobně jako u HQQF-55-503W-4-2, jsem i nyní použil jako výkonové tranzistory unipolární IRFP240 a IRFP9240.
Sluchátkový zesilovač
Dále nabízím zajímavou možnost, použít zesilovač jako sluchátkový, jehož konstrukce se nemění, dojde jen k použití méně výkonného zdroje a menšího chladiče. Samozřejmě bude zesilovač zamontován do menší skříně.
Zapojení a grafy
Rozsah regulace ±20dB
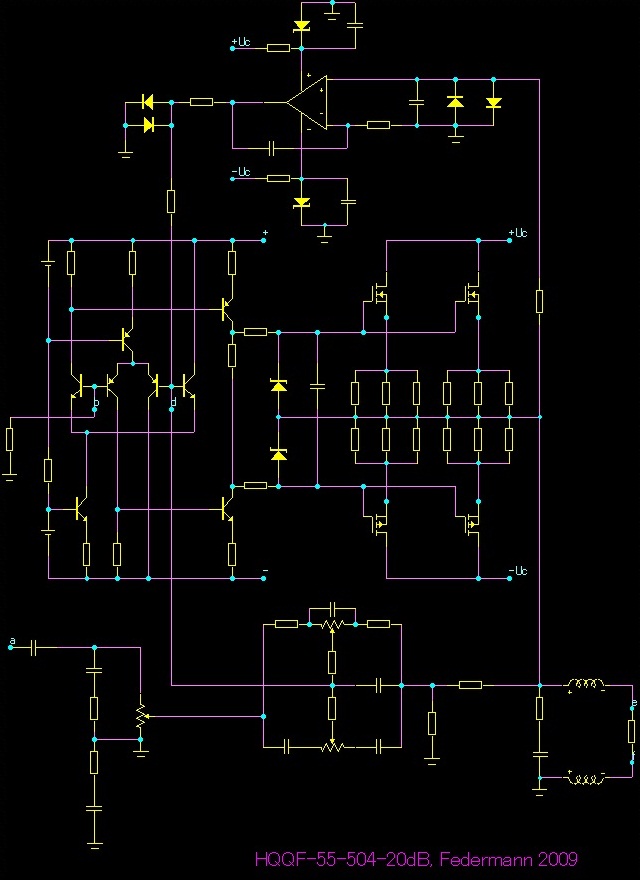
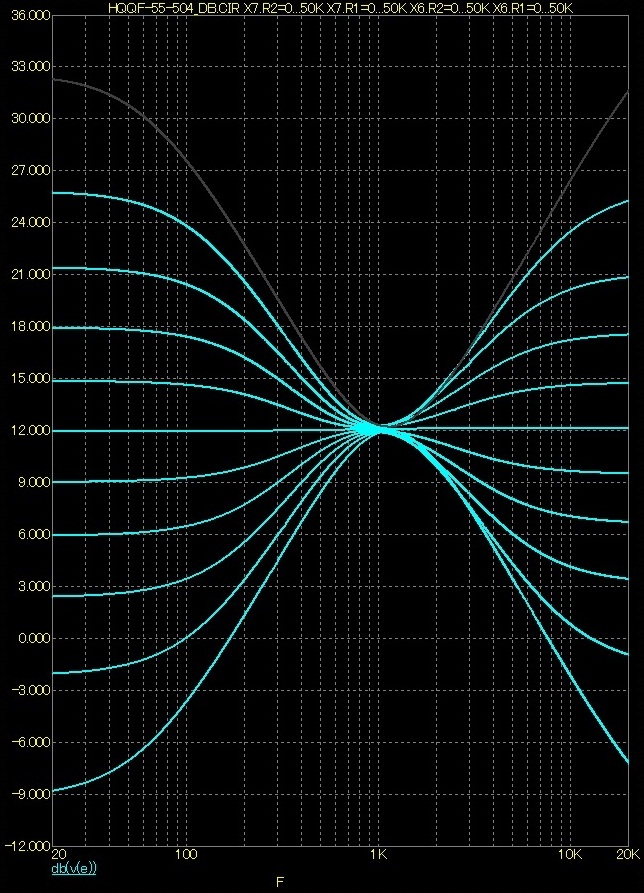
Rozsah regulace ±15dB
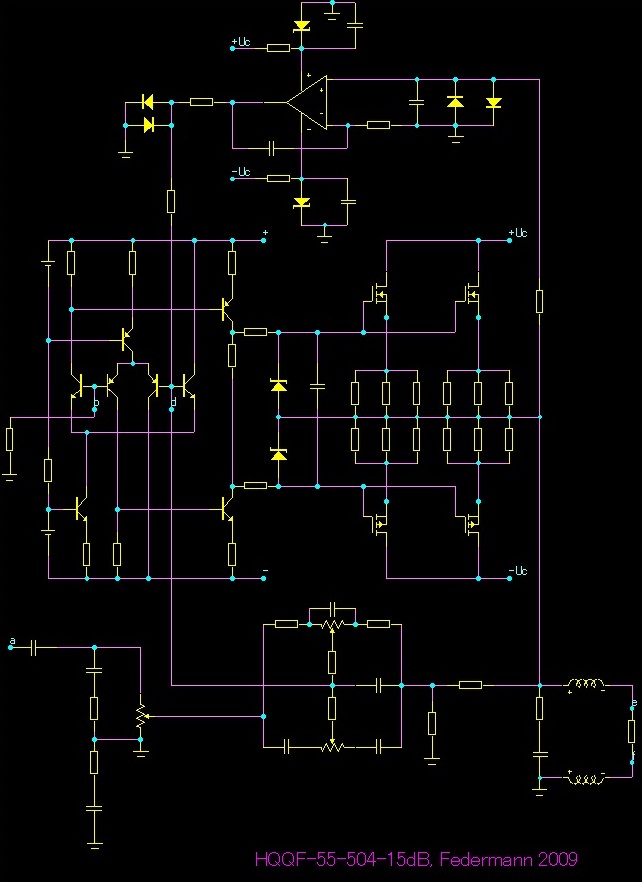
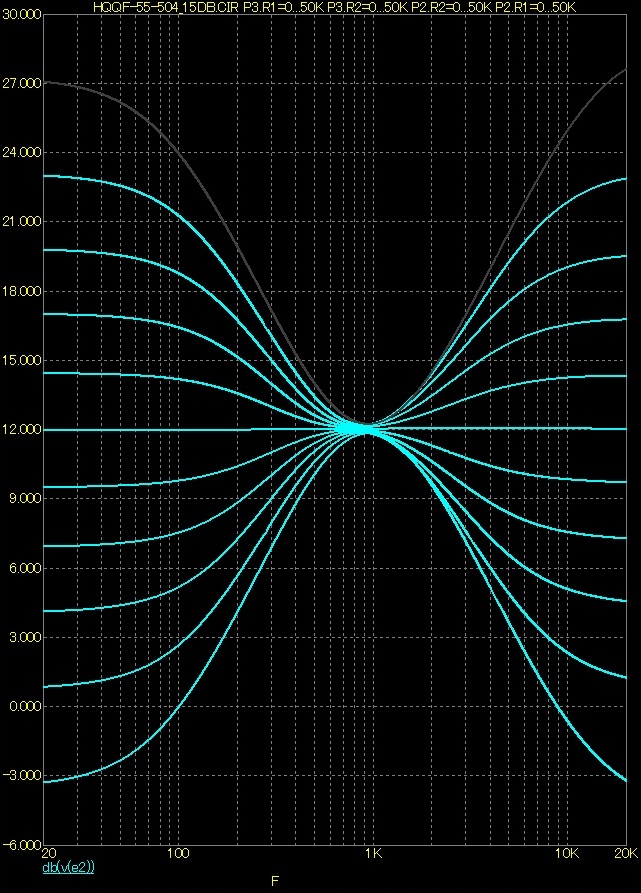
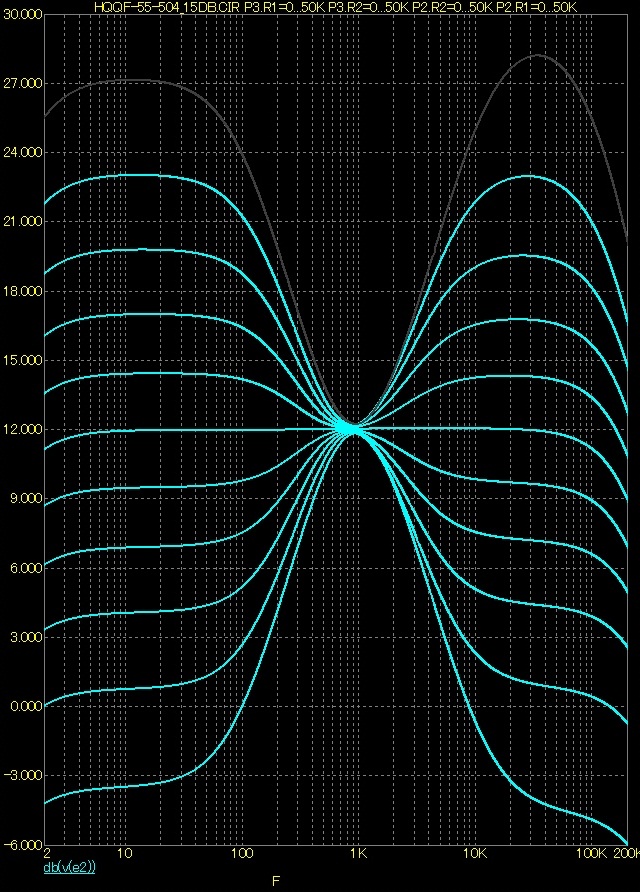
Závěr
Srovnávat obdobné zapojení nelze, neboť není zvykem, aby některý z konstruktérů navrhnul korektor jako součást výkonového stupně. Oddělené řešení je vždy náročnější na počet prvků, ale má také více zdrojů šumu a zkreslení.
Rozdíl, mezi mnoha konkurenčními zapojeními korekčního zesilovače nelze ani komentovat, postačí srovnat charakteristiky a šumové vlastnosti. Většina zapojení je realizována s OZ a jejich zpracovávaná úroveň je cca 100mV, zde se pracuje s úrovní řádu 1,55V.
Zapojení jako sluchátkový zesilovač je naprosto unikátní a to ze dvou důvodů. Zapojení je dostatečně výkonově dimenzováno a navíc má možnost regulace výšek a hloubek, což běžné, ale i špičkové sluchátkové zesilovače postrádají.
Předzesilovač
Část předzesilovače není zatím zveřejněna, ale měla by skýtat možnost použít mikrofon s citlivostí řádu 2mV až možnost připojení na linkový vstup s úrovní 1,55V, čímž vznikne velmi univerzální řešení.
Vlastnosti tranzistoru
Nejdříve se podíváme na vlastnosti tranzistoru. Nebudu zde rozebírat kompletní grafický ani početní výpočet, který snad někdy popíši v samostatném článku. Pro potřeby Topologie Federmann postačí, když se budu zabývat dynamickými vlastnostmi, lépe řečeno napěťovými a fázovými poměry.
Zjednodušený model Tranzistoru Federmann
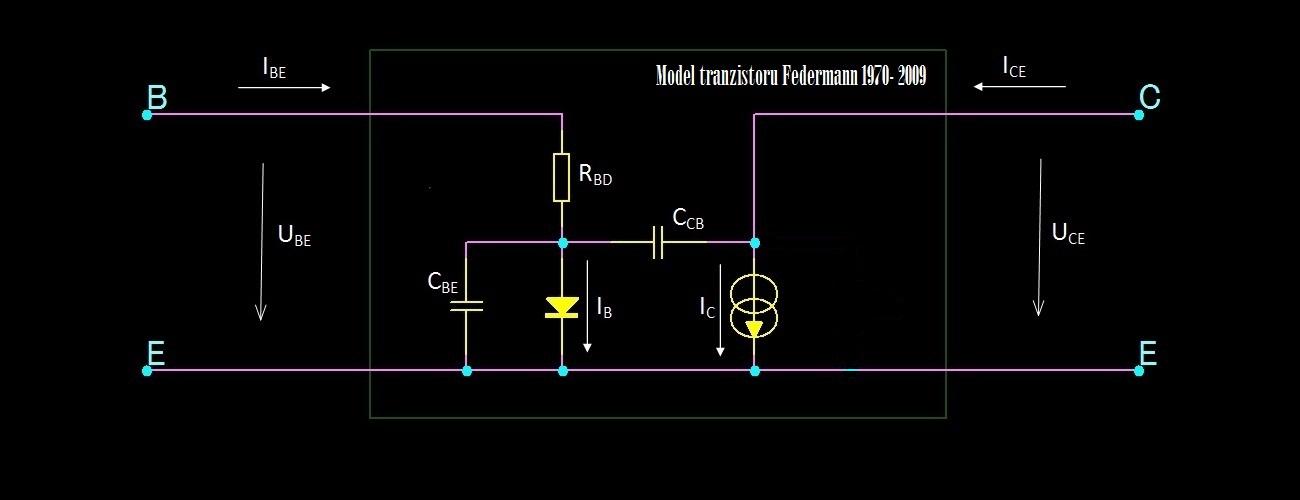
Pro vysvětlení se podíváme na použitý model tranzistoru a uvědomíme si, že odpor RBD je zapojen do série s kapacitou CBE a proud diodou, tedy vlastním přechodem báze-emitor teče v závislosti na napětí na CBE. Připomínám, že jde o zjednodušené výpočty, které jsou na pochopení poměru na přechodu tranzistoru dostačující. Dále se podíváme na obecný R-C člen a na jeho charakteristiky.
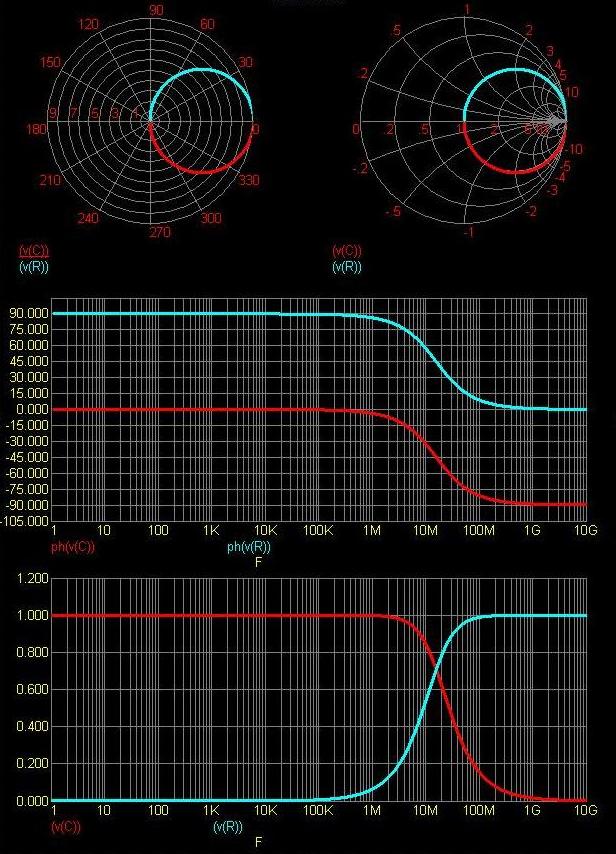
R-C člen

Můžeme si vynést všechny možné závislosti, které se týkají R-C členu. Můžeme si vynést přenosovou charakteristiku i charakteristiku fázovou v závislosti na frekvenci. Zajímavější je charakteristika v polárních souřadnicích či Smithův diagram, ne všichni se však dokážou dostatečně v těchto grafech orientovat.
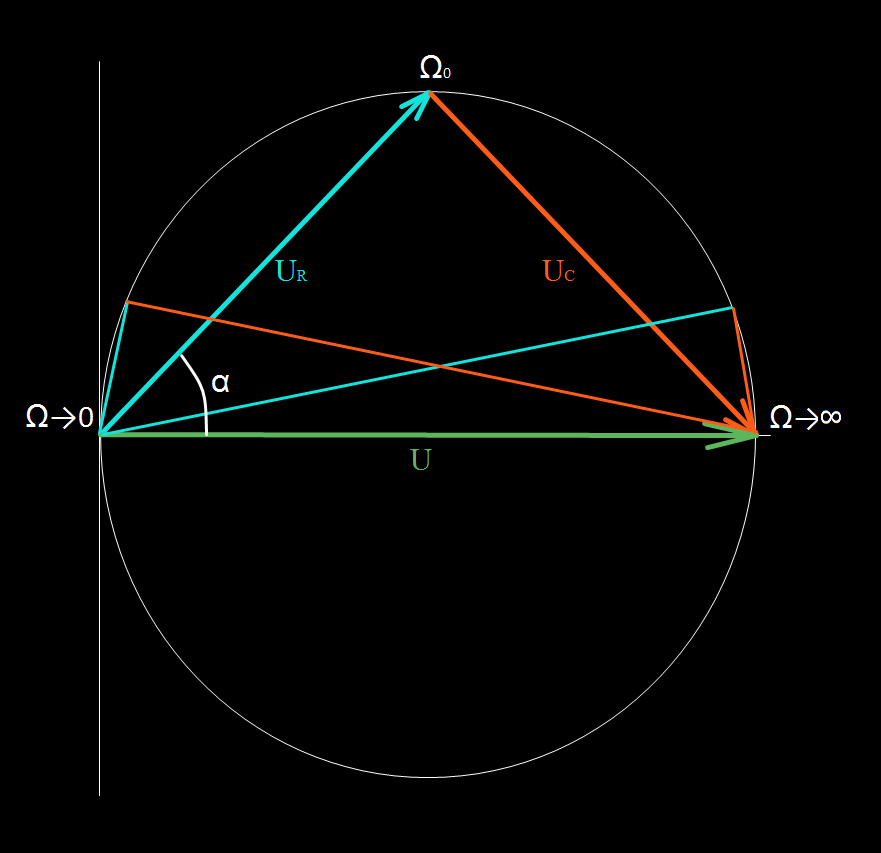
Vektorové vyjádření
Osobně používám nejraději opět vlastní vyjádření a to za pomocí vektorů.
-
Celkové vstupní napětí U vyneseme v reálné rovině a vektorový součet napětí UR a UC mu musí být vždy roven, viz Druhý Kirchhoffův zákon.
-
Pro Ω0 budou obě napětí stejné, znázorněno na vrcholu Thaletovy kružnice.
-
Pro Ω→0, tedy nulový kmitočet, bude napětí UR fázově posunuto o +90°, ale bude nulové, znázorněno na levé straně Thaletovy kružnice.
-
Pro kmitočty blížící se k nekonečnu, bude napětí UC fázově posunuto o -90°, ale bude rovněž nulové, znázorněno na pravé straně Thaletovy kružnice.
-
Úhel mezi napětím UR a UC je vždy 90°, proud obvodem má stejnou fázi jako napětí UR.
-
Takto si můžeme velmi rychle a velmi jednoduše znázornit a vypočítat hodnoty napětí pro Ω, 2Ω, Ω/2 a další kmitočty.
-
Za pomocí Pythagorovy věty vypočteme jednotlivé napětí a amplitudy.
-
Pomocí sínů a cosínů vypočteme všechny potřebné fáze.
Samozřejmě muže každý uvedené hodnoty odečítat s výše uvedených grafů a mnou používaný vektorový graf nepoužít, výsledek bude totožný, jen přehlednost a názornost se změní.
Využití v Topologii Federmann
Nyní se podíváme, jak se dá tento zdánlivě banální poznatek o R-C členu využít v samotné topologii.
Počet stupňů
Počet stupňů nám určuje počet aktivních prvků v signálové cestě. Pokud si za každým aktivním prvkem představíme dva R-C členy, které nám natáčí fázi, pak počet těchto R-C členů vynásobený -90° určuje maximální možné zpoždění výstupního signálu.
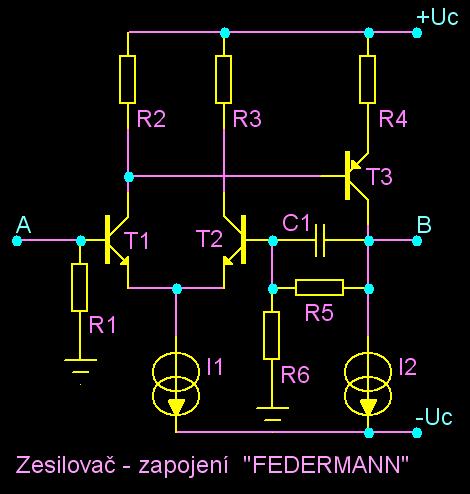
Topologie Federmann
Na modelu zapojení je patrné, že má pouze dva stupně, každý stupeň je zapojen jako inverující, tedy výstupní fáze je opět nulová. Pokud přidáme frekvenční závislosti tranzistorů, pak může výstupní fáze dosáhnout při nekonečném kmitočtu a nulové úrovni výstupního napětí, hodnoty zpoždění -180° na každém tranzistoru.
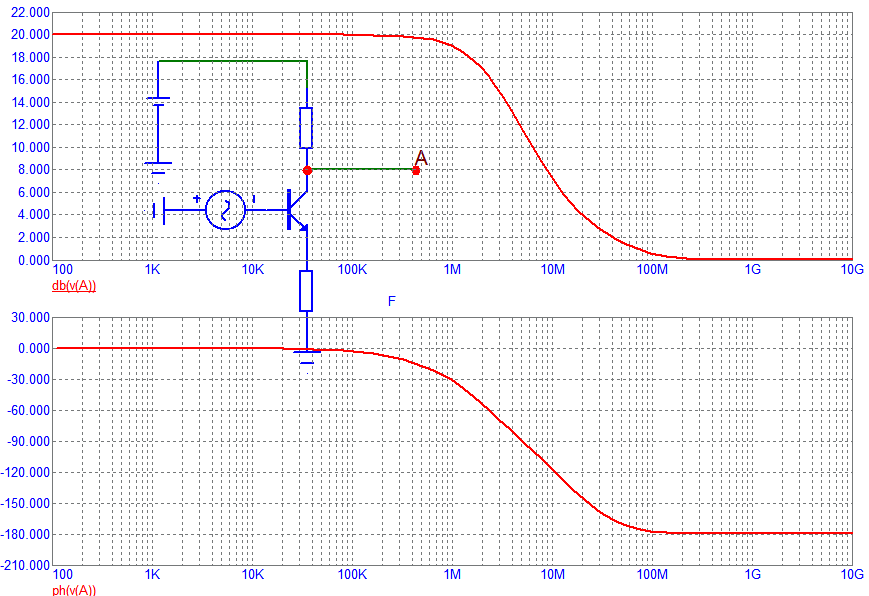
Podmínka oscilace
Podmínka oscilace je:
-
Amplitudová: |AU*|*|β| ≡ 1
-
Fázová: αA + αB ≡ 2Kπ
AU* = Vyjadřuje zesílení otevřené smyčky
β = Vyjadřuje velikost zpětné vazby
Stabilita
Jak je patrné, i kdybychom zavedli zpětnou vazbu jedno-tranzistorové zapojení bez dalšího zásahu není schopno splnit ani napěťovou ani fázovou podmínku oscilace, není možné, aby se rozkmitalo a je naprosto stabilní.
Oscilační podmínka
Při více stupních je zřejmé, že zpoždění signálu, které v konečném důsledku natáčí fázi procházejícího signálu, může dosáhnout až -180°, pak se nám záporný vsup chová jako kladný a oscilační podmínka může být splněna.
Výběr aktivních prvků
Přidání dalšího stupně sebou nese nutnost mnohem náročnější volby aktivních prvků spojený s nutností řešit stabilitu za pomocí lokálních zpětných vazeb na úkor celkové zpětné vazby!
Další a další stupeň
Je patrné, že přidání každého dalšího stupně posouvá kmitočet kdy dojde k celkovému natočení fáze o -180° do výrazně nižších kmitočtů a má negativní dopad do stability celku.
Vlastnosti OZ
Na grafech jsou charakteristiky OPA132, kde je patrné, že většina výstupní fáze je -90°.
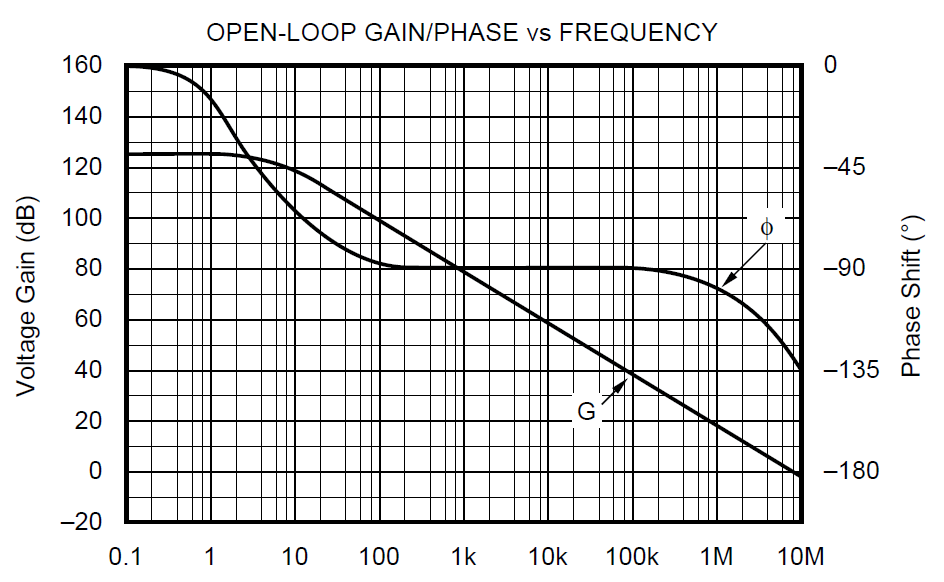
Doplněno
Podívejte se na články se stejnou tématikou.
Úvod
Po dvou úvodních článcích, které byly zaměřeny na některé základní principy Topologie Federmann, na vlastnosti tranzistoru, jeho náhradní schéma a na popis chování R-C členu, kterým ve své podstatě každý tranzistor je.
Dnes se podíváme na konkrétní odlišnosti a dopady použití celkové zpětné vazby a lokální zpětné vazby, výsledek bude pro mnohé rozhodně zajímavý.
Celková zpětná vazba
Abychom mohli dostatečně využít vynikající vlastnosti celkové zpětné vazby, musíme vliv všech lokálních zpětných vazeb dostatečně potlačit. Zde si musíme uvědomit, že každý tranzistor, jeho vstupní odpor RBD, jeho kapacity CBE a CCB nám tvoří lokální zpětné vazby, k těmto prvkům musíme přidat vliv všech připojených obvodů.
Přestože se bavíme o celkové zpětné vazbě, vliv vynucených lokálních zpětných vazeb je nezanedbatelný a musíme si je co nejvíce uvědomovat, jen tak můžeme sestavit takovou topologii, která nebude na těchto nežádoucích, parazitních zpětných vazbách příliš závislá.
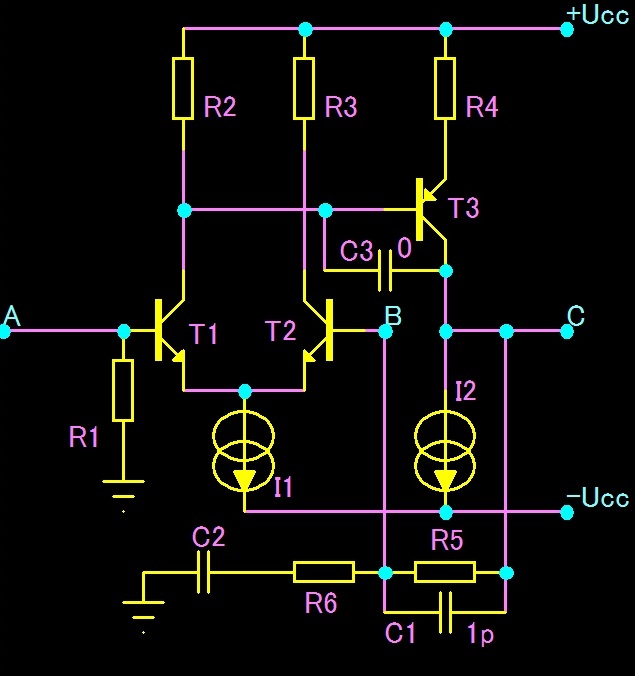
Zapojení
Pro účely posouzení vlivu celkové zpětné vazby použijeme obdobné zapojení jako u Modelu Federmann. Kapacitu C1 použijeme pro celkovou zpětnou vazbu a kapacitu C3 pro lokální zpětnou vazbu.
Sic zůstává kapacita C3 trvale připojena je její hodnota nastavena na 0pF. Dále budeme krokovat jen kapacitu C1 a sledovat změnu charakteristik.
Kapacita C2 ovlivňuje spodní konec přenášeného pásma, proto ji volíme pro tyto účely dostatečně velkou, aby nám neovlivňovala celkovou charakteristiku zesilovače.
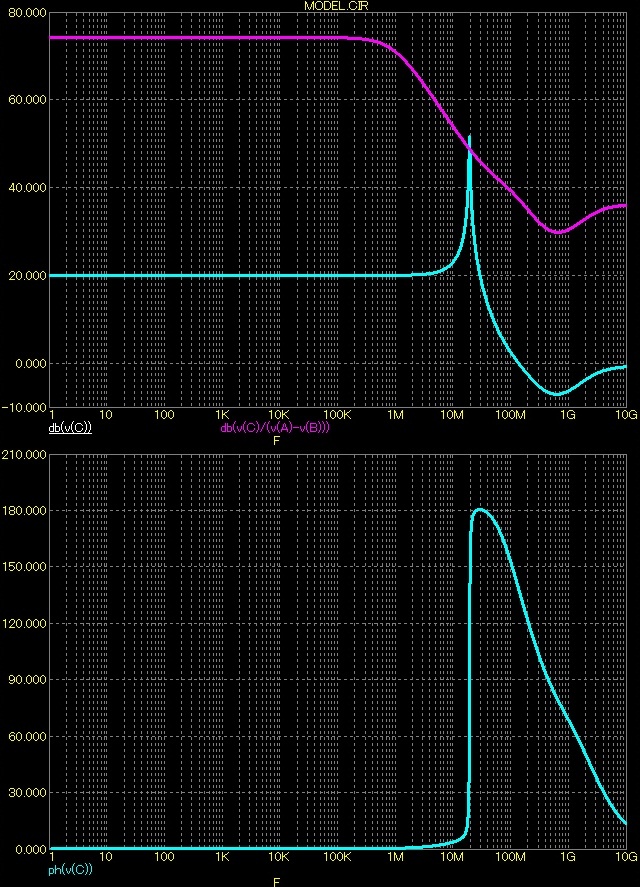
Statické nastavení
Zde můžeme vidět charakteristiky při C1=0pF, kde je patrné, že výstupní napětí mění na kritickém kmitočtu velmi strmě svou fází od 0°po 180°.
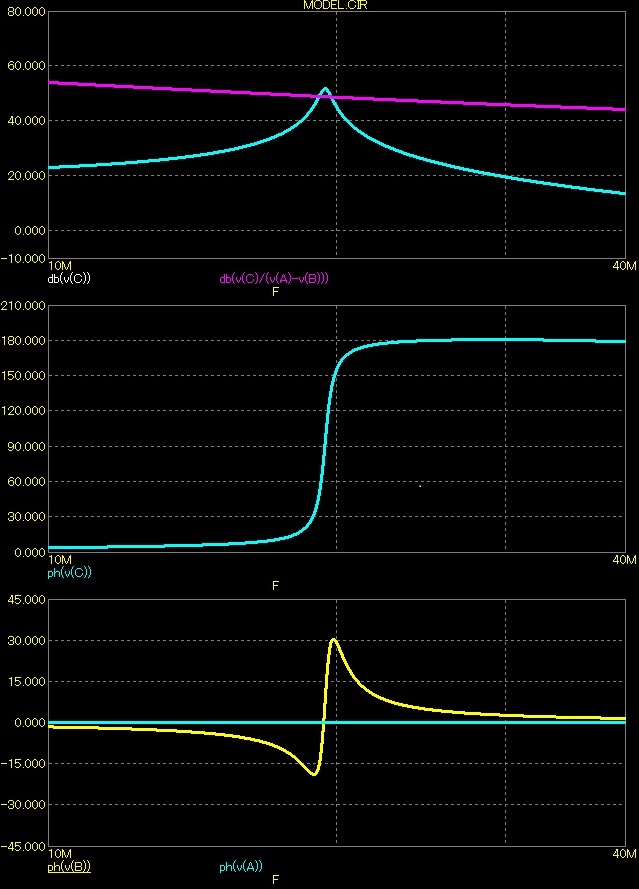
Na grafech níže je detail, abychom lépe pochopili poměry v zesilovači. Mohlo by se zdát, že zesilovač bude náchylný na kmitání, proto jsem udělal i detail poměrů na neinvertujícím i invertujícím vstupu, jak je patrné nikdy nenastává oscilační podmínka, ba co víc je zesilovač dostatečné vzdálen, když se vstupní fáze nedostane ani přes 30°. Je však vidět, že na krátký okamžik se dostává přenosová charakteristika nad AU*.
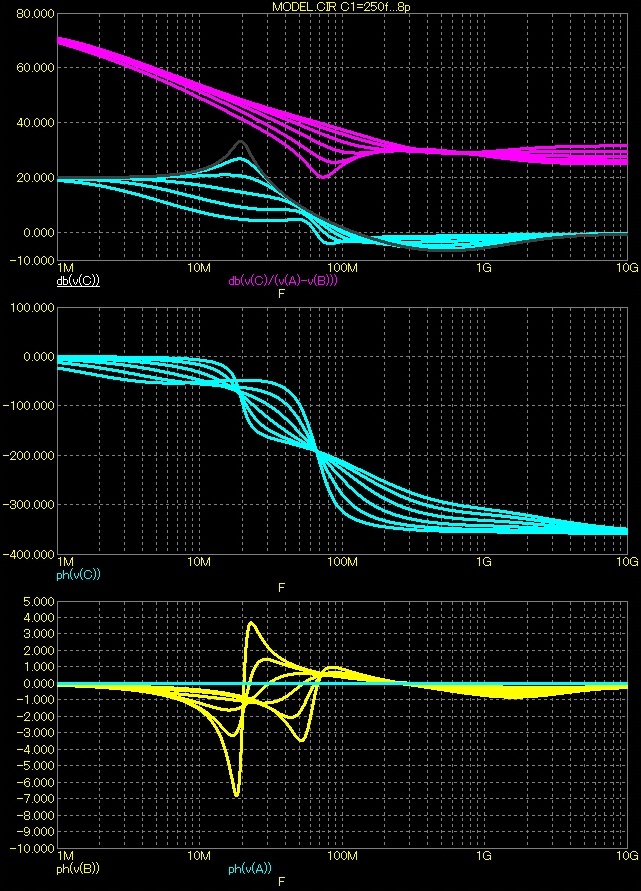
Krokování
Zde se již můžeme podívat, jak to dopadne při krokování kapacity C1 v rozmezí 0,25-0,5-1-2-4 a 8pF.
Mění se nám tvar přenosové charakteristiky na horním konci přenášeného pásma, ale ponechal jsem i pohled na to co se děje se zesílením v otevřené smyčce AU* zesilovače. Je vidět, že AU* se nikterak výrazně nemění.
Na grafu níže se můžeme podívat, jak to vypadá s průběhem Udif a fázovými poměry na obou vstupech zesilovače.
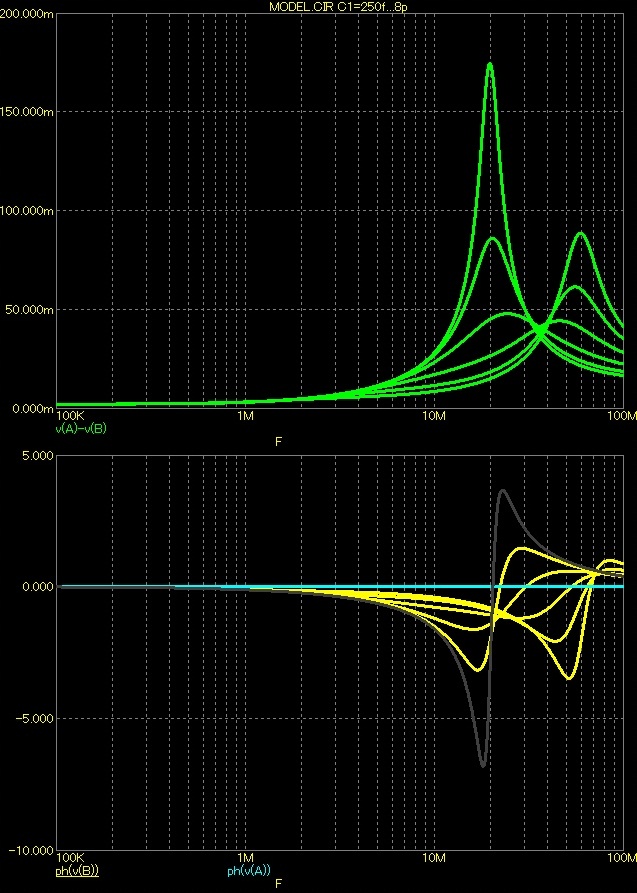
Zapojení s lokální zpětnou vazbou
- Již legendární zapojení od Marshalla Leacha mělo lokální zpětnou vazbu. Používání lokální zpětné vazby se pak stalo módní záležitostí a používali ji téměř všichni. V konečném důsledku mělo zajišťovat lepší stabilitu, ale stejného výsledku by se bylo dosáhlo použitím tranzistorů s výrazně nižší šířkou pásma.
- Polská stavebnice má řešenou lokální zpětnou vazbu za pomocí dvou kapacit, jejichž vliv se pak sčítá.
- DPA od Pavla Dudka má těchto vazeb hned několik, na kolektorech diferenciálních stupňů je s frekvencí zvětšující se zátěž a druhá zajímavě řešená lokální zpětná vazba je za pomocí malé kapacity a spolu s ní napěťově závislé kapacity, která je realizována za pomocí diody.
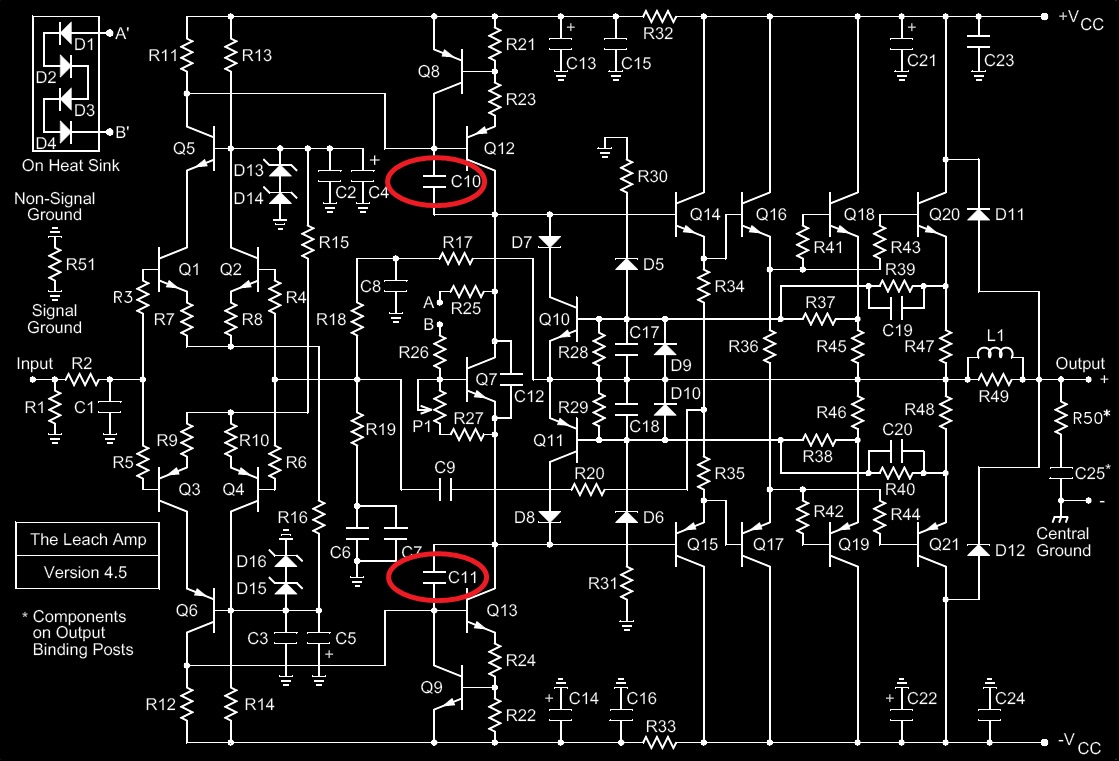
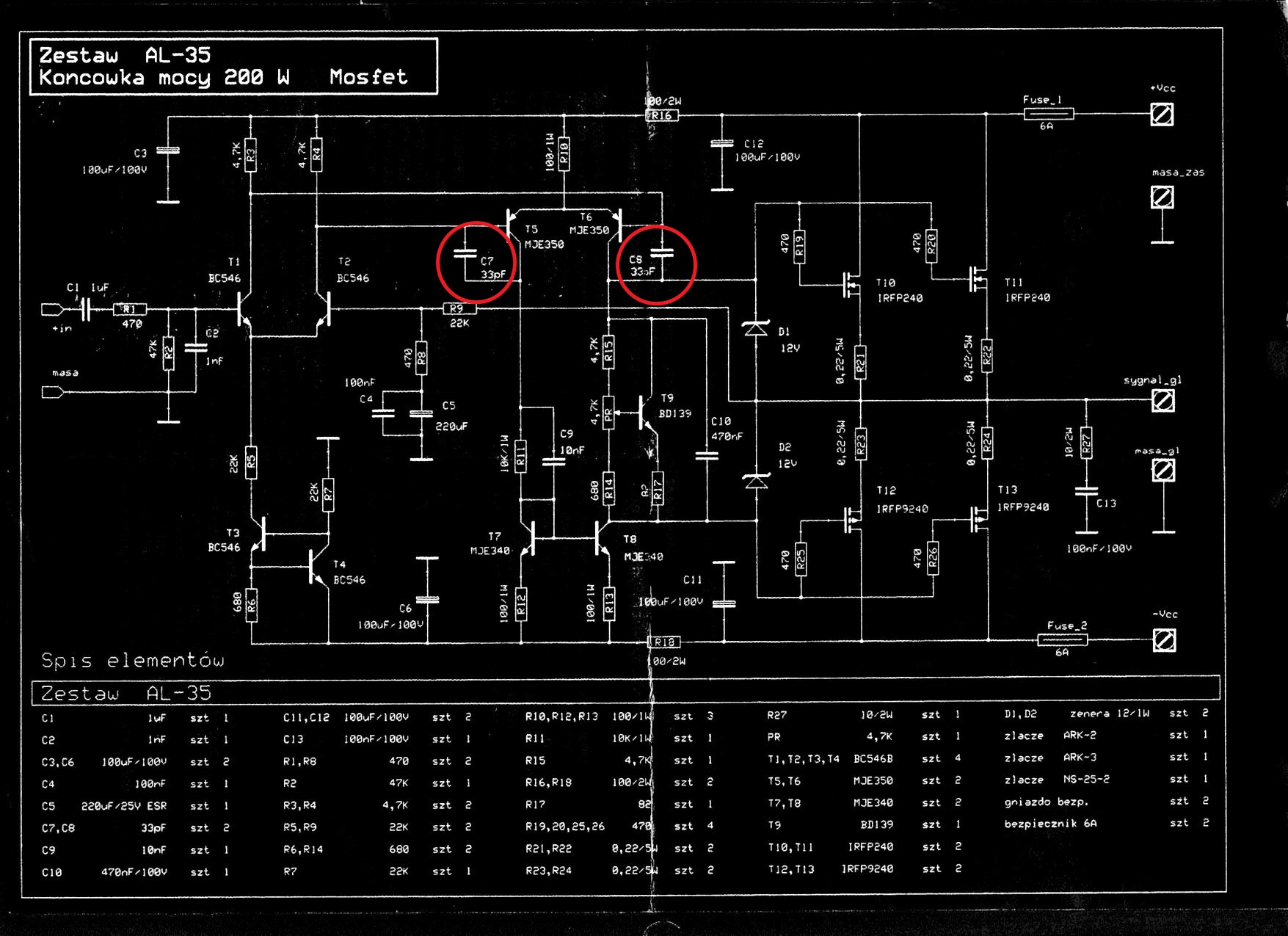
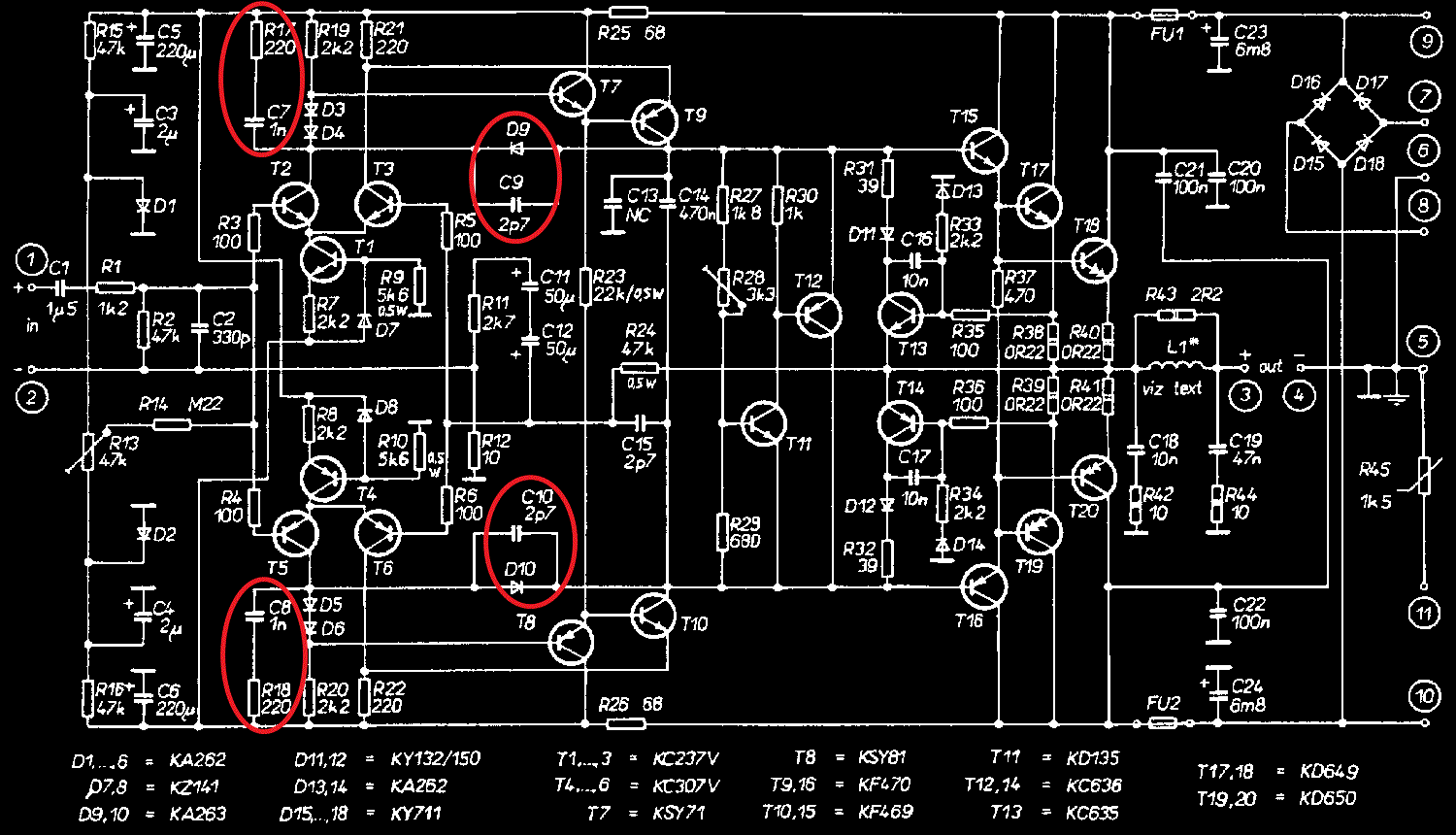
Lokální zpětná vazba
Krokování poprvé
C1 volíme 0pF tím vyřadíme frekvenčně závislou část celkové zpětné vazby a pustíme se hned do krokování kapacity C3.
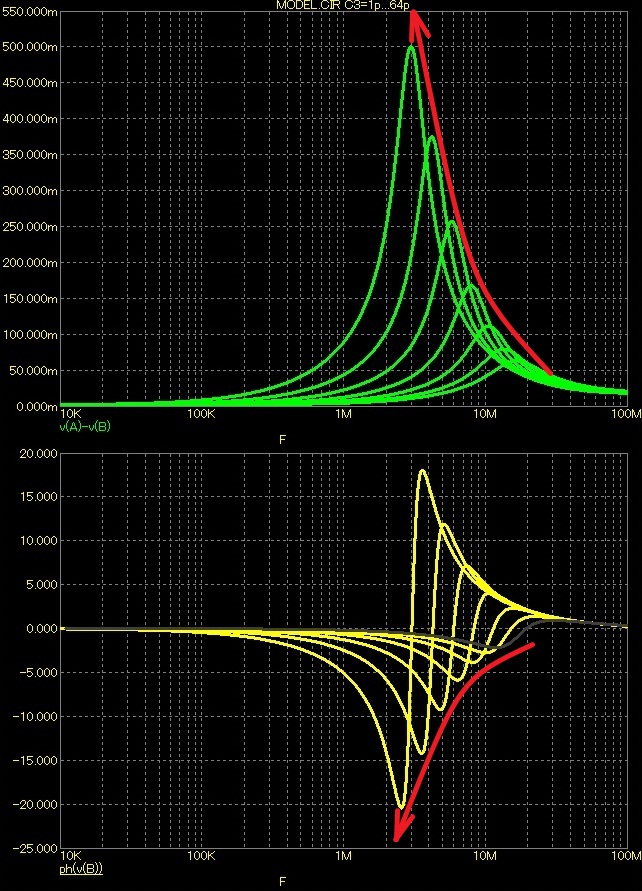
C1 vyřadíme a C3 krokujeme v rozmezí 1-2-4-8-16-32 a 64pF. Přidání lokální zpětné vazby má však na zapojení katastrofální dopad.
Již pro kapacitu 1pF se zapojení stává značně nestabilní a zisk vysoce převyšuje AU*, Udif skokem dosahuje 12V. Při zvyšování kapacity C3 se poměry nepatrně lepší, ale pro normální provoz jsou spíše destruktivní!
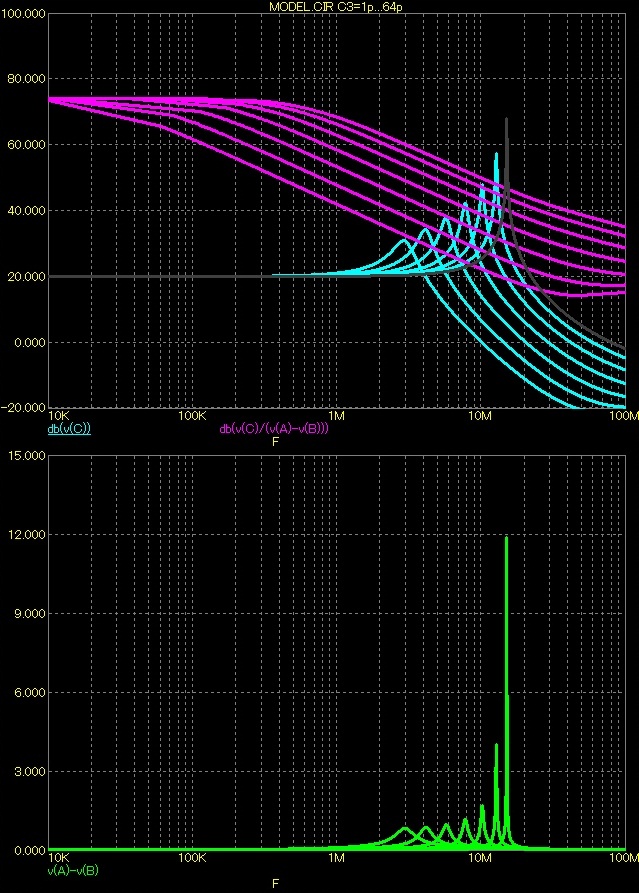
Krokování podruhé
Aby bylo zapojení funkční, vrátíme C1 o velikosti 1pF, kde je průběh dle předchozích grafů pěkně vykompenzovaný.
Nechávám krokovat C3 podruhé a výsledek se dostavuje. Frekvenční pásmo se omezuje velmi pěkně, ale omezuje se i AU*, což není příliš dobré. Na spodních grafech je dále znázorněn dopad do Udif a fázových poměrů, který je rovněž velmi významný.
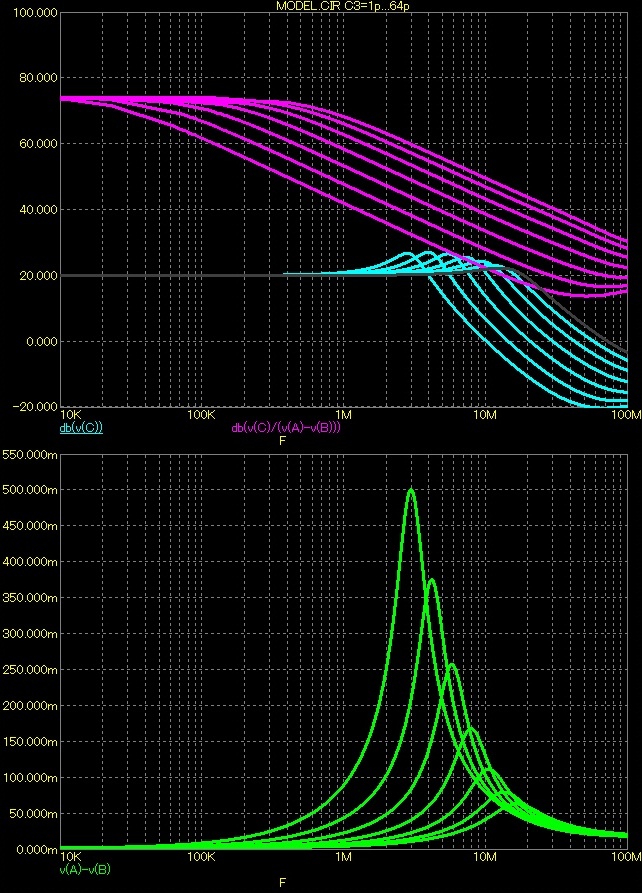

Závěr
Máme za sebou první konkrétní srovnání vlivu lokální a celkové zpětné vazby a měli bychom dojít k nějakému konkrétnímu závěru. Pro tyto účely se podívejme na dopad celkové a lokální zpětné vazby.
Celková zpětná vazba
Zvyšující-se zpětnovazební kapacitou C1 se snižuje mezní kmitočet, aniž by se výrazněni měnilo zesílení AU*, výsledkem je zvyšování rezervy AU* na mezním kmitočtu. Udif se nám posouvá naopak k vyšším kmitočtům, stejně tak jeho fázové natočení.
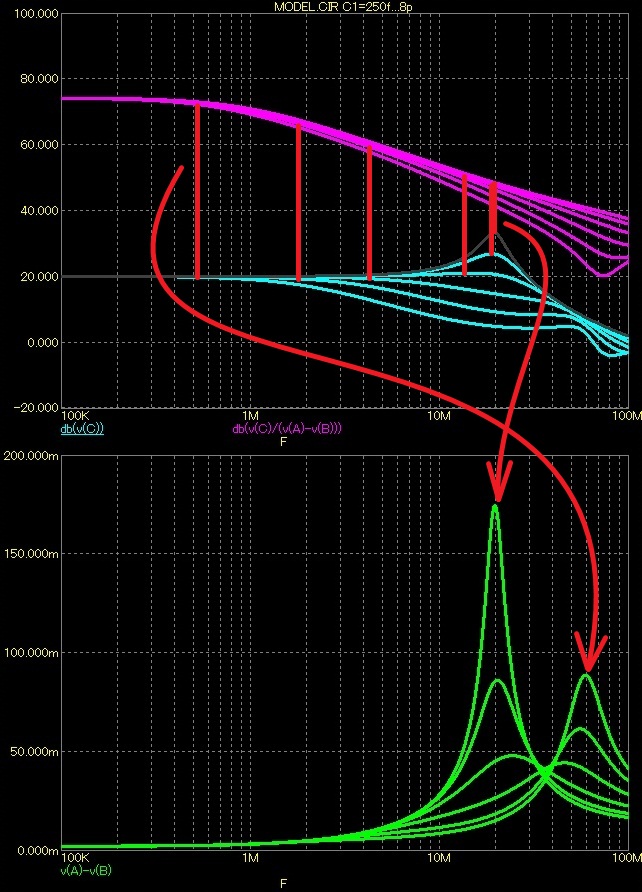
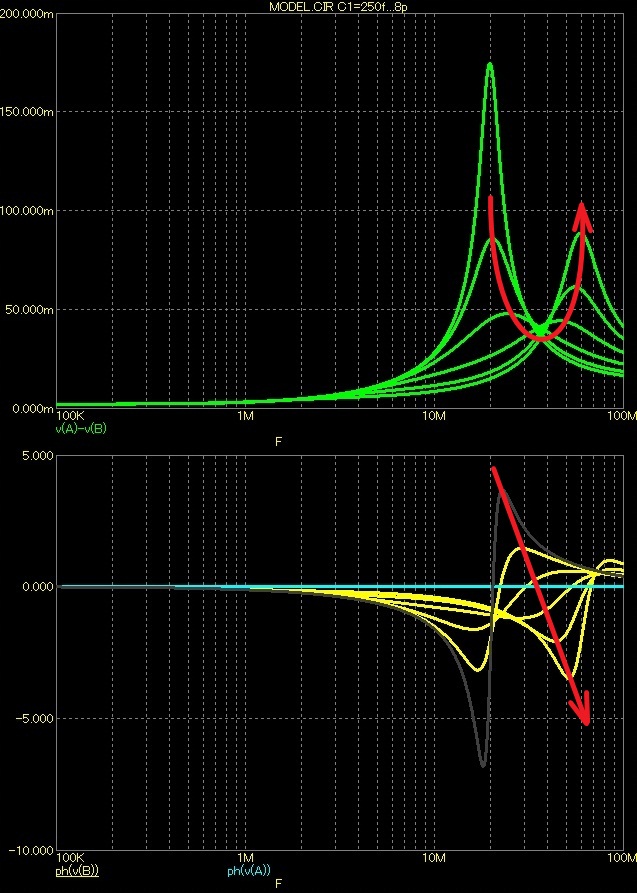
Lokální zpětná vazba
Zde to vypadá naprosto jinak. Zvyšující-se zpětnovazební kapacitou C3 se rovněž snižuje mezní kmitočet, ale jeho pokles je mnohem elegantnější, což u celkové zpětné vazby nedosáhneme.
Potud ta příjemnější část vlivu lokální zpětné vazby. Pokud se podíváme dále, pak zjistíme, že pokles zesílení na mezní frekvenci je doprovázen výrazným poklesem zesílení AU* a samozřejmě výrazným nárůstem Udif a zhoršením fázových poměrů Udif.
To vše se nám v konečném důsledku projeví jako obrovský nárůst zkreslení pod mezní frekvencí a činnost diferenciální dvojice v silně nelineární oblasti.
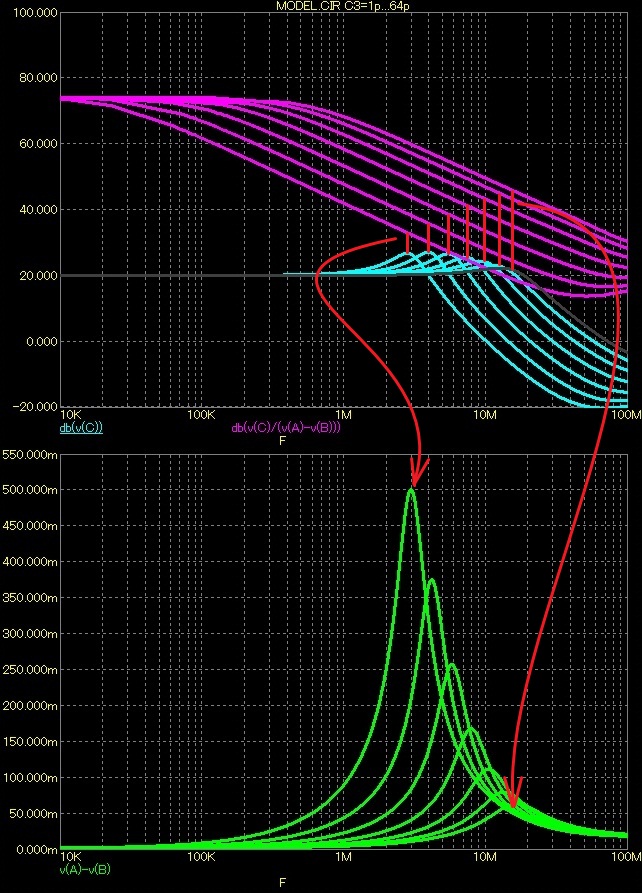
Dovětek
Mnohé se dá vyjádřit matematicky a vypočítat. Fázové poměry na vstupech diferenciální dvojice jsou úměrné zpoždění, ale taky odklonu od vrcholu průběhu.
Pro sinový průběh by platilo:
Z fázového posunu Udif=(UB*(1-cosinus α))/AU
Z rezervy AU dostaneme Udif=UB/( AU*-AU)
Závěr k Celkové zpětné vazbě
Jde o velmi elegantní řečení, ale je nutno si uvědomit, že regulace šířky pásma, za pomocí zpětnovazebního kondenzátoru není ta pravá. Nejlépe je nastavit šířku pásma takovou jaká při konkrétním zapojení vyšla, tedy průběh optimálně vykompenzovat.
Z prvního obrázku je patrné, že pro šířku pásma do 100kHz je charakteristika dokonale rovná a kritický kmitočet je cca 20MHz. Pro lepší průběh Udif je vhodné použít cca dvojnásobný zpětnovazební kondenzátor. Pro konkrétní případ by to bylo ne 1pF, ale cca 2pF. Šířka pásma se z cca 20MHz sníží pod 10MHZ a vrchol Udif přesune z cca 20MHz na cca 50MHz.
Další omezení šířky pásma je zapotřebí provést nejlépe vřazením příslušného pasívního filtru do signálové cesty před samotný zesilovač. U zapojení by se daly najít bez kapacity C3 dva uzly, cca 20MHza 70MHz, ale o tom někdy příště.
Závěr k Lokální zpětné vazbě
Možná nekonečné zkoušky typu pokus omyl v minulosti mnohým přinesli zdánlivě dobrý výsledek, obzvláště když byl jejich poslech omezen jen na CD nahrávky, které si navíc sami ještě za pomocí různých limitérů silně zkomprimovali.
Pro kvalitní Hi-Fi zařízení je však tato cesta jen špatně použitelná. Pro případy více stupňových zesilovačů se situace nikterak výrazněji k lepšímu nezmění, spíše naopak.
Doba krásných nahrávek na magnetofon s předmagnetizací daleko přes 200kHz a vinyl nesoucí informaci o signálu daleko přes 100kHz, musela na chvíli ustoupit CD, které se spokojily jen s 20kHz. Ale vše se jednou končí, opět se frekvenční pásmo vrací daleko nad 100kHz a s ním i spousta problémů kolem zesilovačů. Jeden z nich je právě použití lokální či celkové zpětné vazby.
Pokračování brzy a bude stále zajímavější...
Podívejte se na články se stejnou tématikou.
Předmluva
V minulosti jsem již mnohé prozradil. Nejdříve se jednalo o zapojení Federmann a vůbec jsem nepředpokládal, tak značné odlišnosti od konkurenčních řešení.
Sám jsem vycházel z topologii vzniklých v 70. letech minulého století a dříve, které jsem dále rozvíjel. Konkurenční řešení jsem sice znal, ale nepovažoval jsem je nikdy za významné.
Model Federmann

Zde jsem mnohé popsal, ale popis sloužil spíše jako výklad některých principů studentům:
Úvod
Postupně se rozvinuly ne vždy lichotivé diskuse a stále více jsem si uvědomoval obrovskou rozdílnost pohledu na priority různých zapojení. Všechna konkurenční řešení se hnala za extrémně malým zkreslením a trvale maximálním výkonu.
Můj pohled byl značně odlišný, používal jsem méně aktivních prvků a žádné lokální zpětné vazby tvořené pomocí kondenzátorů. Konkurence se snažila vysvětlovat, že právě jejich řešení za použití mnoha tranzistorů a stupňů, doplněných řadou frekvenčně závislých zpětných vazeb je to pravé řešení, ke kterému bych měl dospět. Nikdy nezapomněli ani používat ultra-lineární tranzistory, o kterých to tvrdili alespoň výrobci, a jejich cena byla značně nadprůměrná.
Nikdo nechtěl pochopit, že právě toto řešení jsem před více jak 30roky definitivně zavrhl. Teorie na obou stranách pokulhávala a Tranzistorový zvuk byl pro mnohá strašákem a pro jiné zdrojem posměchu. Čas běžel a postupně jsem popsal některé souvislosti, hlavně je doložil za pomocí SPICE_kompatibile programů. Pomalu jsem skládal mozaiku a první výsledky se začaly dostavovat.
Nejdříve si však bylo nutno ujasnit některé fakta:
- V článku Kouzelné Watty a Dynamika se doplnil obraz potřebného dynamického rozsahu.
- V článku Vnímáme infra a ultra zvuk? se upřesnil potřebný frekvenční rozsah.
- V článku Nepostradatelná barva tónů a jeho reprodukce jsme si ukázali, že frekvenční rozsah reproduktorů byl a stále je dostatečný.
- Ale v článku Tranzistorový zvuk a VIP a AudioWeb jsme si ukázali, že vývoj a zvyklosti posledních 30let jsou tak pevné, že někteří na žádná fakta neslyší. Než by si poopravili svůj názor, raději se obrní a zakážou na takové témata vést diskuze a všechny příznivce jednotně zavrhnou.
- Následoval článek Dynamická saturace, příčina Tranzistorového zvuku! ve kterém jsem mnohé vysvětlil a popsal. K tomuto článku vzniklo velmi mnoho materiálu a z časových důvodů byla použita jen malá část. Další materiály budu postupně dle časových možností zveřejňovat.
- Dále vznikl velmi zajímavý text SACD, blíže vinylu?, který popisuje vnímání barvy tónů a vyšších harmonických.
- Jako poslední významnější text jsem napsal Zesilovače a fakta o jejich konstruktérech, kde rozebírám vývojové chyby posledních mnoha let.
- Neměl bych opomnět ani článek THD a SR, zapomeňte!, věnovaný pohledu na provázanost THD, SR, výstupního napětí a zpoždění zesilovače.
Úvod do Topologie Federmann
Tím máme malou rekapitulaci za sebou a můžeme pokročit k samotné problematice Topologie Federmann. Ukážeme se čím se tak výrazně liší a v čem jsou hlavní odlišnosti.
Tranzistor
Nejdříve se podívejme, jak se běžně vyučuje tranzistor a jeho náhradní model. Nedalo mi, abych se nepodíval i na stránky vysokých škol a nepodařilo se mi najít pro mne přijatelný model tranzistoru, který by popisoval jeho dynamické vlastnosti. Všechny modely tranzistoru řeší statické vlastnosti a o dynamických se toho moc nedovíme, přitom modely, které používají SPICE programy, jsou téměř dokonalé, ale pro běžného čtenáře nečitelné.

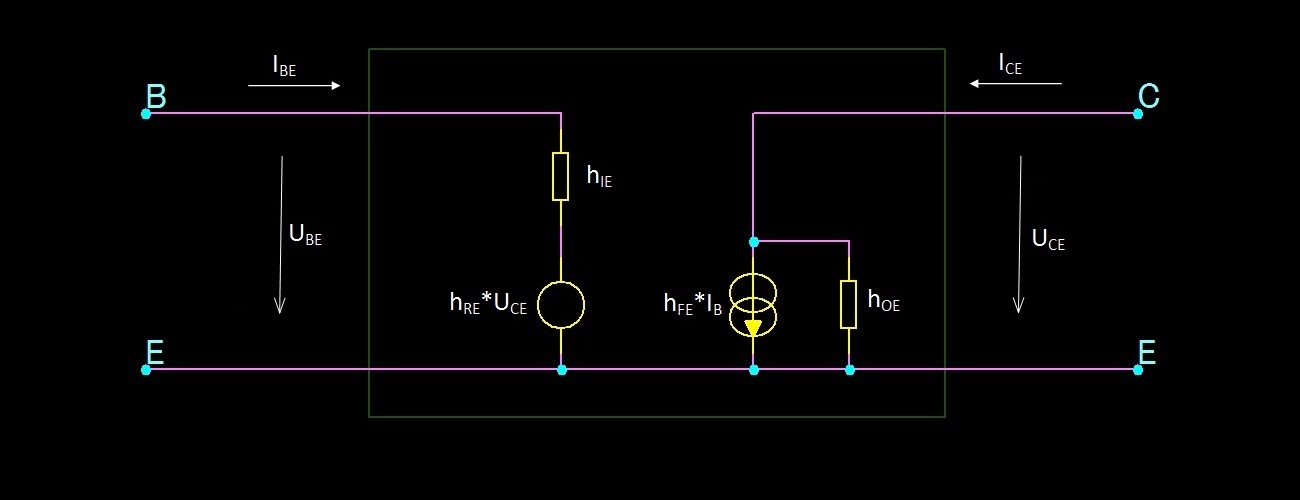
Tranzistor – Model Federmann
Pro účely objasnění dynamických i statických parametrů používám dlouhá léta vlastní model tranzistoru. Model je velmi jednoduchý a má návaznost na fyzikální pochody uvnitř tranzistoru.
- RBD odpor báze dynamický, který se vypočte jako ΔUBE/ΔIBE
- CBE je kapacita přechodu BE
- CCB je kapacita přechodu CB
Pro mnohé zjednodušené výpočty model bohatě postačuje a dá se na něm i něco počítat. Elegantně se dělá v grafech.

Simulace vnitřních dějů
Pro simulace jsem použil stále stejné staré zapojení. Byly simulované proudy diferenciálním stupněm a odvozováno Udif. Jednotlivé body jsou označeny a je patrné co se měřilo.
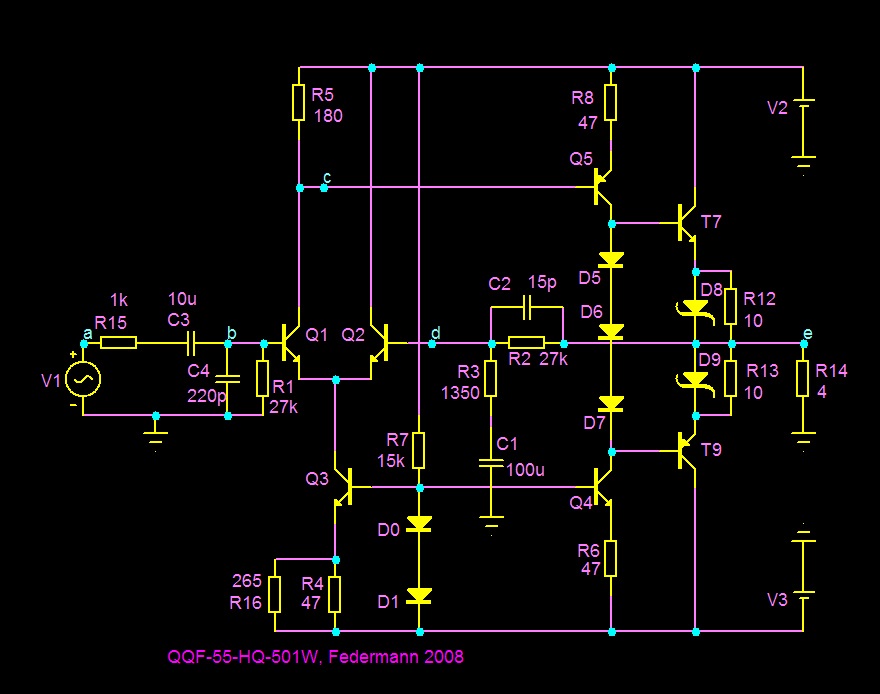
Grafy
Při simulacích byl krokovaný zpětnovazební kondenzátor C2 a to v rozsahu 1-2-4-8-16-32 a 64pF. Na spodním fialovém grafu je patrná změna šířky pásma. Zelený graf výše ukazuje závislost velikosti diferenciálního napětí Udif, kde je pěkně vidět, že se zvětšováním kapacity se Udif zmenšuje a zplošťuje, ale ne zas tak jednoznačně, nevhodnější průběh je pro kapacitu kolem 30pF a pro kapacitu 64pF je velmi malé Udif na cca 200÷300kHz, ale nepříjemně se nám zvedne na 10MHz.
Za pozornost stojí i žlutý průběh na přiloženém grafu dolů, na kterém je překrásně znázorněn průběh napětí na kolektoru prvního tranzistoru diferenciální dvojice. Zde je patrné, že průběh tohoto napětí přesně koresponduje s průběhem Udif. Dá se tedy dovodit, že nárůst Udif není zapříčiněn poklesem zesílení diferenciální dvojice T1 a T2, ale tranzistory následovnými.

Světová premiera
Nesmím opomenout ani diskusi HifiSlovanet dosáhl významného úspěchu!, kterou jsem otevřel poté, co jsem vytvořil své první vlákno na diyAudio s názvem Topology Federmann, HQQF-55 .... Vlákno se začalo nebývale rychle rozvíjet, jenže ne směrem vysvětlování jednotlivých principů a detailů, ale muselo čelit soustavným útokům Česko-Slovenských rádoby konstruktérů.
Podstatná část útoků musela být vymazána a vlákno nakonec zamčeno. Mělo to dokonce pokračování, kde museli moderátoři udělit i týdenní BAN jednomu s útočníků. Útoky však splnily účel, aby mohl být představen konkurenční projekt bez kapacitních lokálních zpětných vazeb.
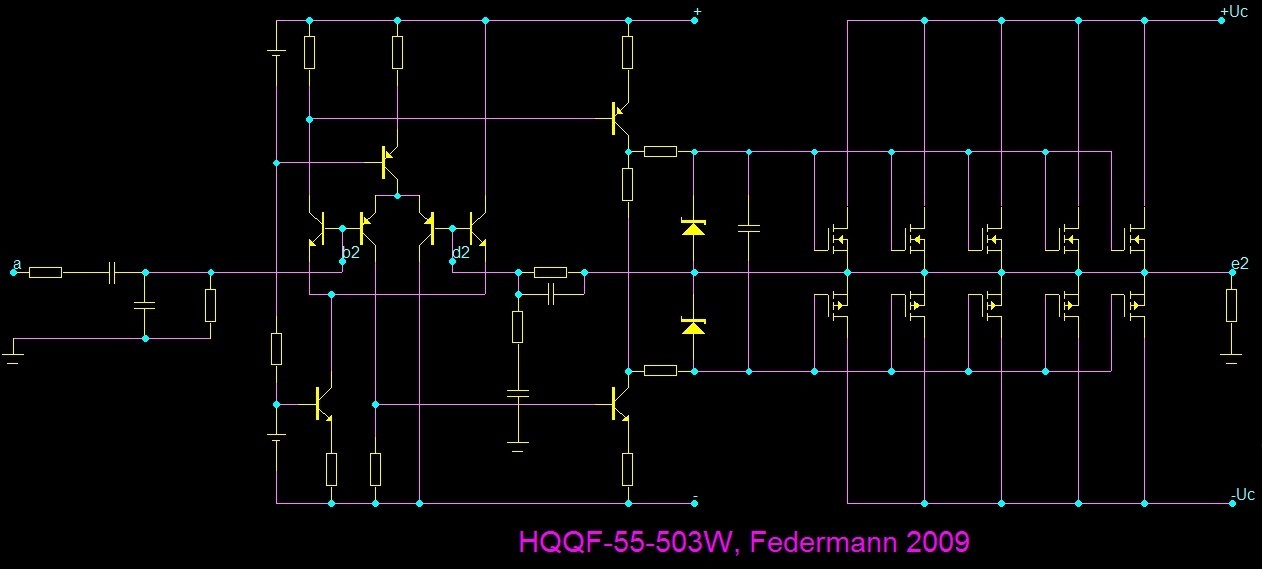
Je vidět, že konkurence se rychle učí a začíná si některé kroky osvojovat, proto jí nebudu v poznání bránit, ale naopak ukážu další chyby, kterých se neustále dopouští a čím je Topologie Federmann, Topologii Federmann.

Podívejte se na články se stejnou tématikou.
Rubriky
L
Nejnovější
- HQQF 2 x 510-514 v jedné skříni
- HQQF 2párová levná verze
- Audio - Koronavirus a pětašedesátníci
- Genealogy of the genus Federmann
- Bastlírna - všeuměl Team boss EKKAR, nyní As vs. Ws
- Novinky Hi-Fi světa 09/2019
- Transiwatt pod palbou Trolů podruhé
- Transiwatt pod palbou Trolů
- Federmannovo zkreslení
- I MISTŘI se mýlí, aneb 50let slepé cesty po desíti letech
- Ochrana zesilovače
- Bastlírna - všeuměl Team boss EKKAR PC a step down
- Bastlírna - všeuměl Team boss EKKAR PC expertem
- Bastlírna - všeuměl Team boss EKKAR Lingvistou
- Bastlírna - všeuměl Team boss EKKAR trapně perlí
- Bastlírna - všeuměl Team boss EKKAR a Curieova teplota (Tc)
- Ceník zesilovačů III. tisíciletí, zesilovačů HQQF (únor 2019)
- Bezpečnostní rizika v Česku, aneb konec volné soutěže
- Bastlírna a všeuměl Team boss EKKAR stále perlí ...
- Závěrečný 23. článek v Praktické elektronice AR 12/2018
- Již 22. článek v Praktické elektronice AR 11/2018
- 7nm AMD finišuje v TSMC, Intel stále v nedohlednu
- Moduly a díly audio-zesilovačů
- Již 21. článek v Praktické elektronice AR 10/2018
- Jubilejní 20. článek v Praktické elektronice AR 09/2018
- Horko a Team boss EKKAR opět na EB radí
- 19. článek v Praktické elektronice AR 08/2018
- 18. článek v Praktické elektronice AR 07/2018
- Topologie Federmann opět hýbe internetem?
- 17. článek v Praktické elektronice AR 06/2018
- Rébus s ECC81 a opět EKKAR
- Ceník zesilovačů III. tisíciletí, zesilovačů HQQF
- USA odstupují od jaderné dohody s Íránem, světová ekonomika se otřásá v základech!
- 16. článek v Praktické elektronice AR 05/2018
- 15. článek v Praktické elektronice AR 04/2018
- 14. článek v Praktické elektronice AR 03/2018
- Internetové reakce na PE-AR květen 2018, EKKAR stále ve střehu
- NOVIČOK a konspirace?
- Petro-Yuan přichází, konec hegemonie dolaru?
- Elektronkový předzesilovač HQQF-55-510 opět trochu jinak
- Předzesilovače a charakteristiky RIAA stále dokonaleji a stále jinak
- RIAA dnešních dnů vs. Actidamp, EKKARovy rady nadevše
- Je všechno jenom náhoda?
- 13. jubilejní článek v Praktické elektronice AR 02/2018
- Malé ohlédnutí nejen za rokem 2017...
- 12. výroční článek v Praktické elektronice AR 01/2018, PF 2018
- DIN stále žije
- 11. článek v Praktické elektronice AR 12/2017
- Bastlírna opět ve starých kolejích a všeuměl EKKAR opět perlí
- 10. článek v Praktické elektronice AR 11/2017
- Cena Bastlířů 2017 - Vyhodnocení komentuje EKKAR
- 8. článek v Praktické elektronice AR 09/2017
- 9. článek v Praktické elektronice AR 10/2017
- 7. článek v Praktické elektronice AR 08/2017
- Výroba tranzistorů v ČSSR podle EKKARa
- 6. článek v Praktické elektronice AR 07/2017 a co dál?
- Měření FFT, pokořena hranice -300dB!
- 6. článek v Praktické elektronice AR 07/2017
- Proudová ochrana audio zesilovače
- Výroba elektronek v ČSSR podle EKKARa